Неинтуитивная математика: парадоксы карточной колоды

Последний туз

Представьте себе, что вы пришли в казино, и вам предлагают сыграть в новую игру. Возможно, не самую интересную, но вот её правила: дилер берёт в руки колоду и начинает переворачивать карты одну за другой, а вы должны угадать, каким по счёту выйдет последний, четвёртый в колоде туз. Может быть, 25-м или 38-м – можете указать любую позицию. Колода тщательно перемешана, распределение карт в ней случайно. Правильно угаданный последний туз оплачивается одинаково независимо от выбранной вами позиции.

Кажется, трудно придумать плюсовую стратегию для такой игры, ведь в такой колоде тузы могут оказаться где угодно. Однако на самом деле у нас есть оптимальный выбор, который максимизирует наши шансы на победу. Этот выбор –

Выбирая её, вы будете выигрывать в ста процентах случаев.

Шучу, конечно. Вы просто будете выигрывать чаще, чем при любом другом ответе. Давайте разберёмся, почему.

Прежде всего, в этой игре есть очевидно глупые ответы. Нет смысла выбирать первые три карты, потому что это по определению не принесёт вам успеха. Даже если этой картой будет туз, он точно не будет последним в колоде. Нужный нам туз теоретически может выйти где-то между 4-й и 52-й картами.

Допустим, вы выбрали 38-ю карту. В четырёх случаях из 52 вам действительно покажут туза, но вероятность того, что это будет последний в колоде туз, не стопроцентна. Важное отличие выбора 52-й карты в том, что называя её, вы гарантируете: вышедший на этой позиции туз окажется последним.

Чтобы лучше понять, почему это важно, давайте сыграем колодой из шести карт.

Смысл в смещении выбора ближе к концу колоды в том, что чем дальше мы забираемся, тем в большем количестве раскладов выбранная нами карта оказывается четвёртым и последним тузом. Выбирая четвёртую карту, мы побеждаем только в том случае, если предыдущие три туза оказались на первых позициях. Это не строго единственный расклад, потому что мы не учитываем масти. Наши тузы могут выходить в любом порядке, так что у нас есть 24 победных расклада.

Но когда мы выбираем пятую карту, нужных нам раскладов становится больше. Тузы могут перемешиваться точно так же, но на любой позиции до них или между ними также может оказаться любая из двух дам. И ещё больше вариантов нашей победы будет при выборе шестой карты.

Не хочу погружаться в расчёты для 52 карт. Вот, например, все расклады для колоды из трёх карт – с двумя тузами и королём.

Выбирать первую карту, очевидно, не стоит – мы не выиграем ни разу. Выбор второй карты принесёт нам победу в двух случаях из шести. Выбор третьей карты – в четырёх случаях из шести. Вывод очевиден!

Шутки джокера

Чтобы понять условия этой задачи, достаточно знать, как определяется сила рук в покере. Ниже я расставил все комбинации по старшинству, от флеш-рояля до хай-карты.

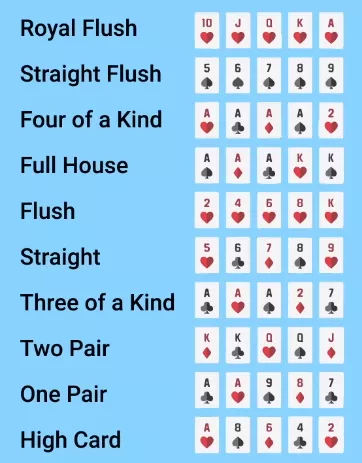
Как известно большинству из вас, старшинство комбинации определяется по вероятности её появления: чем она реже встречается, тем сильнее. Есть всего четыре флеш-рояля, 36 стрит-флешей, 624 комбинации каре и так далее. Общее количество комбинаций превышает 2.5 млн.

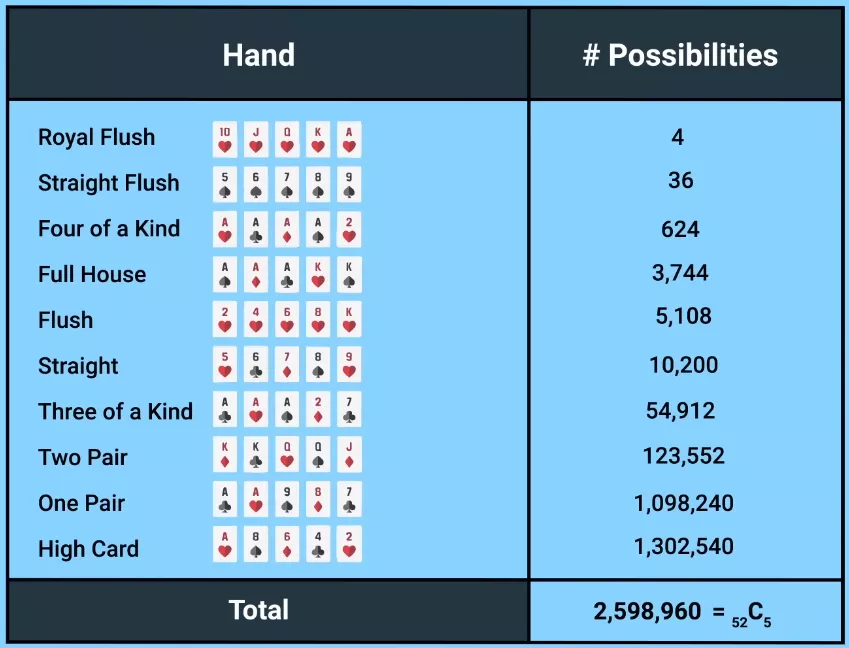
Представим себе, что мы добавили в колоду джокера. В колоде теперь не 52 карты, а 53. Получив на руки джокера, вы можете превратить его в абсолютно любую карту. Конечно, вы постараетесь максимально усилить свою комбинацию. Без джокера рука – это всего лишь пара. С джокером – трипс, если мы превратили его в . Превращение джокера в тоже усиливает нашу руку, но только до двух пар; но мы, конечно, выбираем более сильную комбинацию.

И теперь мой вопрос:

должно ли измениться старшинство комбинаций, когда мы играем с джокером, и если да, то как именно?

Может быть, наличие в колоде джокера сделает флеш менее вероятным, чем фулл-хаус? Может быть, будут ещё какие-то изменения? Одно можно назвать сразу: с джокером появляется комбинация «пять одинаковых карт». Какое место в иерархии она займёт?

Очевидно, что первое: число комбинаций равно количеству номиналов карт в колоде, 13. Флеш-роялей с джокером становится в шесть раз больше, и с 24 комбинациями они опустятся на второе место.

Но других новых типов рук у нас не будет. Так что, изменится старшинство комбинаций из-за джокера или нет?

Надеюсь, вы успели обдумать этот вопрос, потому что сейчас я скажу вам ответ:

Почему так? Из-за парадокса, связанного с трипсами и двумя парами.

Предположим, мы оставили порядок силы комбинаций неизменным: трипсы старше двух пар. В этом случае всякий раз, когда нам раздадут джокера, карманную пару и две другие карты, мы используем джокера, чтобы усилиться до трипса.

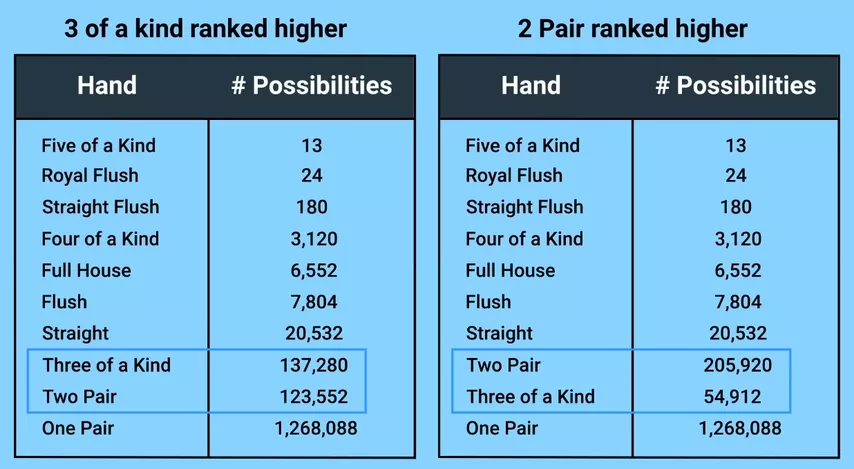
Без джокера трипс можно было собрать 54,912 раз. Из-за джокера их количество увеличивается до 137,280.

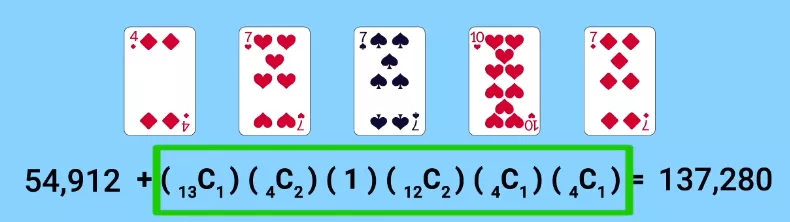
Но это больше числа возможных комбинаций двух пар! Их было 123,552 без джокера, и это число после введения дополнительной карты не изменилось, ведь всякий раз, когда у нас появляется возможность собрать с его помощью две пары, мы предпочитаем трипс, а готовые две пары с джокером всегда превращаются в фулл-хаус.

Раз две пары встречаются теперь реже трипсов, приходится менять старшинство комбинаций. Но тогда игрокам становится невыгодно собирать с помощью джокеров трипсы! Количество трипсов возвращается к начальным 54,912, а число комбинаций двух пар возрастает до 205,920.

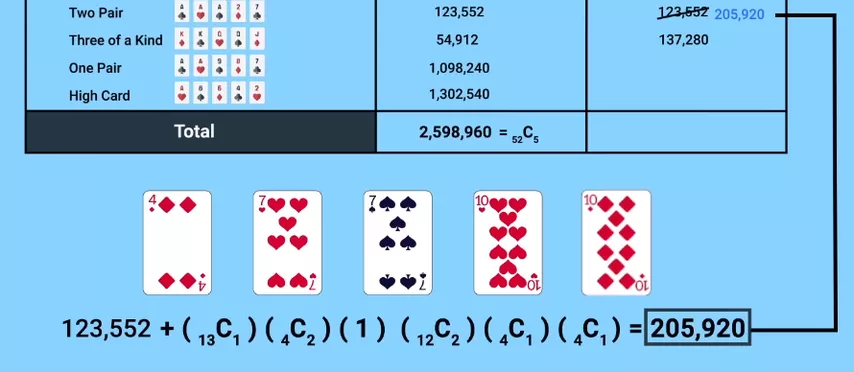
Возникает бесконечный цикл, и мы приходим к парадоксу: окончательно выбрать старшую комбинацию, опираясь на вероятность её появления, становится невозможно.

Если интересно, вот вероятности прихода комбинаций при игре с джокером:

Почти честная игра

Я покажу вам игру, которая на первый взгляд выглядит достаточно честной, однако благодаря простому алгоритму позволит вам выигрывать по меньшей мере два раза из трёх, а при благоприятных условиях – более семи раз против одного.

Играем обычной колодой из 52 карт, половина из которых чёрные, а половина – красные. Участвуют два игрока. Первый выбирает последовательность из трёх карт, называя их цвет, например, «красный – красный – чёрный». Затем то же делает второй игрок. После этого они начинают доставать карты из колоды, и тот, чья последовательность выйдет первой, побеждает.

Вроде бы никакого подвоха. Добро пожаловать в игру Хамбла-Нишиямы!

В октябре 1969 года Уолтер Пенни опубликовал в «Журнале математики для отдыха» простую игру, связанную с последовательностями при выпадении монетки. Вскоре Стив Хамбл и Ютака Нишияма портировали его игру на стандартную колоду карт.

Какие в ней могут быть подводные камни? Ну, наверное, не стоит выбирать последовательность из трёх одинаковых карт, ведь вероятность увидеть третью красную карту после того, как две красные уже вышли, немного понижается. Но что ещё? В конце концов, вероятность выпадения чёрной или красной карты – всегда примерно 50 на 50.

Действительно, если исключить монотонные варианты RRR и BBB, для первого игрока практически нет разницы, что выбирать. Однако у второго есть работающая стратегия, которая гарантирует победу.

Допустим, первый игрок выбрал BRB. Мы берём вторую карту его последовательности, меняем цвет, ставим в начале, убираем последнюю карту – и подстройка готова:

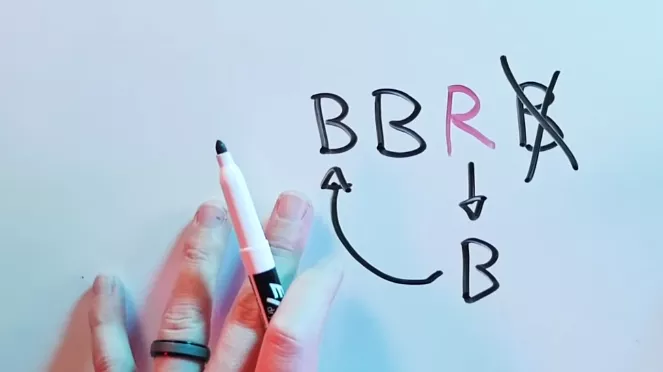
Наше преимущество над первым игроком убедительнее, чем можно предположить в невинной забаве, завязанной на случайном распределении карт:

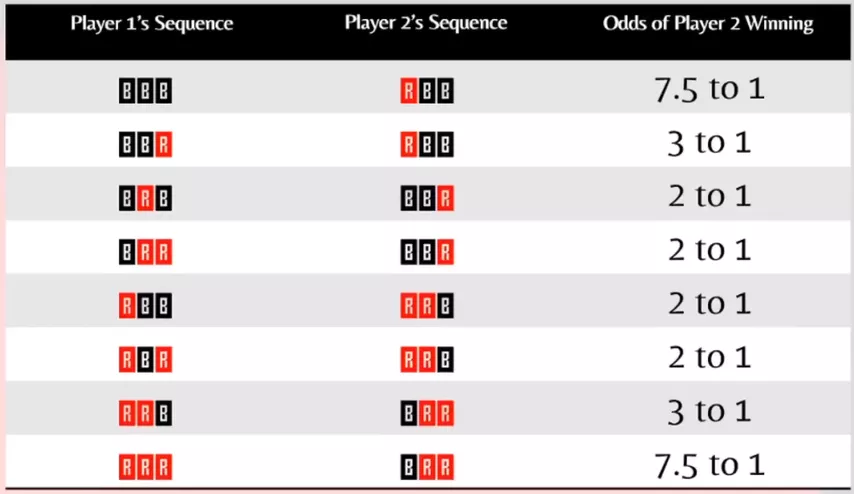
И оно существует, потому что эта игра относится к классу нетранзитивных.

Пример транзитивности:

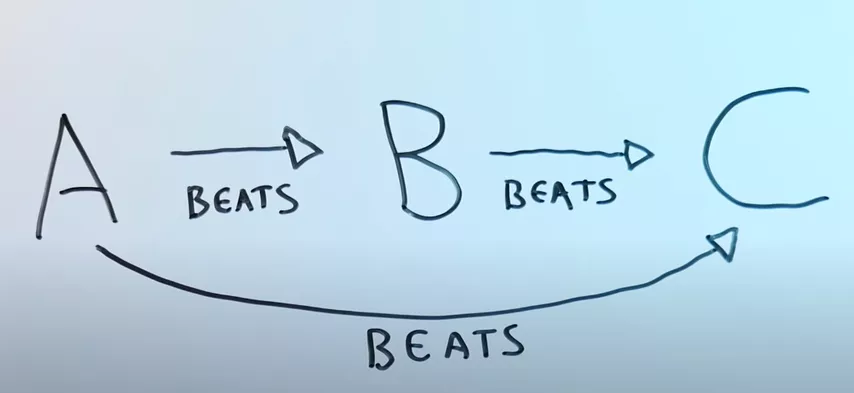
Если вам больше нравится пицца, чем тако, и вы предпочтёте тако собачьим консервам, то и при выборе между пиццей и собачьими консервами вы тоже проголосуете за пиццу. Такие пищевые предпочтения будут транзитивными. Однако если по каким-то неведомым причинам собачья еда для вас вкуснее пиццы (но только в этой паре!), ваши пищевые предпочтения будут нетранзитивными.

В нетранзитивных играх у первого участника нет лучшего выбора. Отношения в них описывают предпочтения на парах альтернатив, сравнение которых приводит к наличию циклов: A предпочтительнее B, B предпочтительнее C, а C предпочтительнее A. Классический пример – разумеется, камень, ножницы, бумага. В этой игре возникает цикл возможных выборов, ни один из которых не даёт лучших шансов на победу.

Игра Хамбла-Нишиямы также является нетранзитивной. Вот иерархия циклов в этой игре:

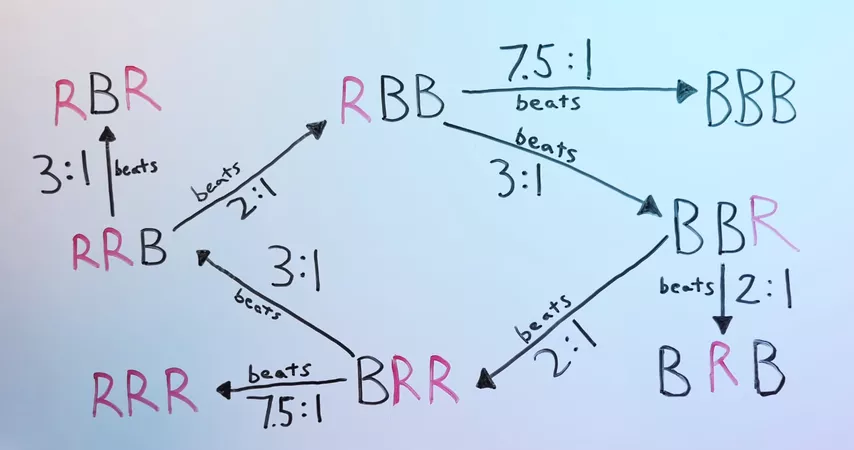
Зная выбор первого игрока, мы можем выбрать наиболее выгодный ответ. И игра, которая на первый взгляд казалась такой честной, на деле даёт второму игроку огромное преимущество.