Давайте немного покопаемся в покерной истории. Тренер Red Chip Poker Адам w34z3l вспомнил теоремы, которые были придуманы нашими предками еще в нулевые. По его словам, в те замечательные времена эти теоремы знали все, кто считал себя профессионалом. Ну, или наоборот, профессионалами считали себя те, кто про эти теоремы знал.
Адам проверил, прошли ли эти древние сокровенные знания проверку временем и можно ли их адаптировать под современные реалии. Из плюсов – запомнить их куда проще, чем правильную частоту контбетов в 3-бет поте, ну, а минус – не все из них работают безотказно. Впрочем, как и все эти солверы.
Теорема Балуга
Это теорема не про большую рыбу семейства осетровых, а про рейзы на терне. Сформулировал ее Эндрю BalugaWhale в 2006 году на 2+2. Звучит она так:
Силу одной пары следует существенно переоценить после рейза на терне
Оригинальный пример из 2006 года:
Мы на UTG с АКo, рейзим 4 bb (сразу чувствуется олдскульный вайб). BTN колл, флоп выходит A93o. Делаем ставку размером в банк (сейчас солвер советует ставить гораздо меньше), оппонент коллирует. На терне выходит 7, пошло флеш-дро. Мы снова ставим пот и получаем рейз.
Теорема Балуга заключается в том, что после подобных рейзов наша топ-пара с топ-кикером смотрится не очень хорошо. Теорема не говорит, что вы непременно должны выкидывать, просто к силе своей руки нужно отнестись очень критически. Ну, и иногда всё-таки сказать «пас», так как довольно часто это окажется верным решением.
Если проанализировать эту ситуацию в солвере, то он почти всегда советует коллировать и рейз на терне, и ставку на ривере. Однако стоит понимать, что после ставки на ривере наши ТПТК – лишь блефкэтчер. EV колла на терне не очень высоко, технически – это колл, который мы играем с целью защиты нашего рейнджа, иначе получится, что мы на тёрне выкидываем слишком часто. Если же в этой ситуации наша рука слабее ТПТК, то солвер будет склоняться к фолду.
В общем, эта теорема достаточно далека от GTO и заточена скорее под эксплойт. Ее идея заключается в том, что средний оппонент не часто делает рейз в блеф на терне. Если посмотреть в Range Research, с чем рейзят терн на NL200 на PokerStars в наши дни, то картина получится такая.
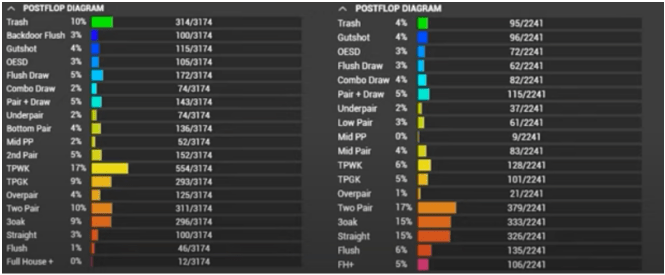
Слева игроки в позиции, справа без позиции
В 58% случаях после чек-рейза у среднестатистического оппонента на руках будут две пары или лучше, а в 70% у него будет топ-пара и старше. Если же оппонент находится в позиции, то вэлью его рук будет почти в два раза меньше – в 25% две пары и старше, а топ-пары и выше – 30%.
По большому счету, можно сказать, что теорема Балуга работает до сих пор. Однако нужно иметь ввиду, что применять ее против чек-рейзов гораздо прибыльнее, так как в позиции игроки чаще рейзят с блефами и полублефами.
Теорема Кларкмейстера
Эта теорема тоже родилась на 2+2. Звучит она так:
Если в хедз-апе на ривере приходит четвертая одномастная карта, и у нас первое слово, то мы должны ставить
Звучит довольно логично. Правда, доказать пользу или вред этой теоремы довольно сложно, так как тут все зависит от конкретной ситуации.
Например, мы без позиции, оппонент контбетит флоп и терн, а на ривере выходит четвертая карта к флешу. В этой ситуации наш донк в блеф на ривере генерирует 57% фолд-эквити и применить теорему Кларкмейстера будет очень выгодно – если мы поставим 75% пота, то чтобы вывести это действие в плюс, нам нужно получить всего 40% фолдов.
Еще один подходящий для теоремы сценарий – когда мы играем проб-бет. Так называется ставка, которую мы ставим против оппонента, который не поставил ставку продолжения на одной или нескольких предыдущих улицах. Тут наша ставка на ривере даст уже 62% фолдэквити. Однако эта ситуация куда менее показательна, так как тут у нас почти всегда много фолдэквити, вне зависимости от карты, вышедшей на ривере. А вот в первом случае четвертая карта к флешу как раз важна, так как в другой ситуации донк не будет столь уж прибылен.
Это конечно не значит, что теорема работает идеально. Если мы трижды ставим без позиции – контбетим флоп, терн и ривер, то в большинстве случаев наше фолдэквити на ривере снизится до 40%. Причем вариант, в котором на ривере выходит четвертая карта к флешу, даже хуже других – в остальных случаях наше фолдэквити 45-50%.
Вывод: Теорему Кларкмейстера можно считать рабочей, но не во всех ситуациях. GTO по поводу этой теоремы не столь оптимистично и ставить в четвертую карту к флешу советует редко.
Теорема Йети
Возникла эта теорема тоже на 2+2, а название получила в честь автора.
3-бет на сухом флопе, особенно спаренном – почти наверняка блеф
Допустим, мы оказались на флопе А72о или КК2о. Наш оппонент ставит контбет, мы делаем рейз. Если он делает ещё один рейз, поверить в силу его руки будет достаточно сложно. В большинстве случае с трипсом королей или сетом семерок, увидев рейз, почти все оппоненты предпочтут слоуплей. Но если все сильные руки на сухих бордах уходят в слоуплей, как тогда выглядит рейндж 3-бета? Он что, полностью состоит из блефов? В наши дни это выглядит как серьезная проблема. А если заглянуть в софт, то окажется, что в наши дни эта теорема просто неверна.
Сейчас средний игрок диапазона блеф 3-бета на флопе практически не имеет, а играть так станут только с железным натсом вне зависимости от текстуры. В выборке с NL200 на сухой или спаренной доске процент блеф 3-бетов и мерджей крайне низок.
Вывод: Теорема Йети проверку временем не прошла. Есть подозрение, что даже в 2005 году она не то чтобы печатала деньги…
Теорема Зибо
Ни один игрок не способен выбросить фулл-хаус вне зависимости от улицы и размера ставки
Тут даже без анализа можно сказать, что это сказки. В подходящей ситуации избавиться от фулла не так уж и сложно, такие игроки есть, и их немало. Особенно, когда на доске лежат две пары, а фулп у нас младший.
Например, возьмем борд 8877х. Если у нас 7х, а оппонент ставит много – фолд в такой ситуации вполне можно рассмотреть. Однако это не делает теорему бесполезной. Если ее немного перефразировать, то она может послужить хорошую службу и сейчас:
Не пытайтесь выдавить игроков из банка, если подозреваете у них сильную руку
Если вы предполагаете, что у оппонента фулл-хаус, то блефовать не стоит. Это касается и стритов, и флешей – если, конечно, нет предыстории, которая позволяет вам полагать, что оппонент способен на сложные фолды. Это определенно не та ситуация, в которой можно выиграть деньги.
Еще один актуальный урок, который мы можем извлечь из этой теоремы – неизвестный игрок скорее переоценивает силу своей руки. Кто-то посмотрит на свои карты и подумает: «Вау, да у меня же фулл-хаус!» Даже если этот фулл доминирован со всех сторон, они будут опираться на абсолютную силу своей руки, не обращая внимания на все остальное. Даже в наши дни таких игроков хватает за столами, особенно на микролимитах.
Теорема АЕДжонса
Была опубликована хайроллером aejones на форуме 2+2 в 2007 году.
Ни у кого никогда ничего нет
В буквальном смысле эту мудрость прошлых веков воспринимать, конечно, не стоит, но перефразировать эту теорему можно так:
У игроков не всегда будет настолько сильная рука, как вы думаете
Эту проблему можно назвать синдромом «монстра под кроватью». Обостряется он обычно во время даунстриков, когда вам постоянно мерещатся натсы у оппонентов. «Конечно, мы поймали младший сет, но у врага то наверняка топ-сет!» Поверить в такое несложно, особенно, если с вами эти ситуации за последние несколько десятков тысяч раздач случаются частенько.
Если мы попробуем абстрагироваться от влияния стриков и посмотрим на общую картину, то окажется, что рука оппонента довольно часто оказывается слабее, чем мы предполагали. В холдеме не так уж просто собрать сильную комбинацию, и если у нас это получается не всегда, то и у наших оппонентов должна быть та же проблема. Об этом полезно помнить, особенно во время даунстрика.
Из этого утверждения можно вывести еще одно, которое не теряет своей актуальности во все времена:
Агрессивная игра гораздо выгоднее, чем пассивная
Не стоит сильно переживать из-за того, что у оппонента в каком-то отдельном случае оказалась сильная рука, ведь это может помешать вам решиться на прибыльный блеф за соседним столом. А иногда вы можете даже удивиться, насколько легко оппоненты готовы расстаться со своими картами.
На этом всё о древних теоремах. Надеюсь, вам понравилось наше путешествие по волнам памяти, и чем чёрт не шутит, может, вы даже извлекли что-то полезное из рассказа о принципах, которые считались незыблемыми в прежнюю эпоху онлайн-покера.
