Я делаю много покерных видео и могу авторитетно заявить, что из всех терминов покерной теории люди хуже всего понимают минимальную частоту защиты – MDF. Вроде бы совсем просто: MDF подсказывает, насколько широко нужно защищаться, чтобы ваш соперник не мог прибыльно блефовать с любыми картами. Однако эту простую концепцию окружает множество мифов, мешающих правильно ею пользоваться. Сегодня мы попробуем исправить положение.
Начнём с простейших случаев.
– Начинающие часто путают MDF с шансами банка. И то, и другое описывает риск и вознаграждение, но в первом случае речь идёт о блефе, а во втором – о колле.
– Случаются ошибки при расчёте MDF, когда мы получили рэйз: люди подставляют значения не в ту формулу. Однако видео об этом я уже записывал и не хочу сегодня повторяться.
Моя сегодняшняя тема – это мифы и концептуальные ошибки.

Мне попадались расчёты MDF, не учитывающие, что у блефов есть эквити. Часто это связано с расчётом тенденций поля. Авторы анализируют данные и говорят: смотрите, поле фолдит чаще, чем MDF! Значит, мы можем блефовать с любыми двумя картами! Увы, они ошибаются – или пользуются неправильной формулой. Когда у блефов есть эквити, MDF считают по-другому.
Более опытные покеристы могут сказать вам, что солвер, играющий по GTO, всегда защищает меньше MDF. Понимаю, почему люди так думают, но и это неправда. И сегодня мы это увидим.
Наконец, нередко встречается утверждение, что MDF не имеет значения до ривера. Вроде бы это примитивная метрика, придуманная для игр с урезанными правилами, в которых у блефов не бывает эквити, то есть её нельзя использовать ни на одной улице, кроме последней. Если вы тоже в это верите, возможно, проблема в том, что вы используете чересчур упрощённое определение MDF.
Давайте поговорим о тонкостях анализа больших баз данных. Если вы давно играете, храните все свои раздачи и пытаетесь по этой базе определить тенденции поля, сравнивая действия игроков с MDF, вы наверняка замечаете, что
1) поле оверфолдит на контбеты флопа;
2) поле слишком широко защищается против рэйза флопа.
Это приводит вас к эксплуатирующей стратегии контбета с любыми двумя картами... но нет, это не слишком рабочая идея. Почему? Да потому что такая игра поля совершенно правильна и, более того, соответствует GTO. Сейчас вы в этом убедитесь.
Допустим, хайджек сделал рэйз, большой блайнд заплатил. Стеки 100 бб. Флоп... неважно, какой флоп, потому что я использую обобщённую статистику по всем флопам. Хайджек ставит контбет 33% банка.
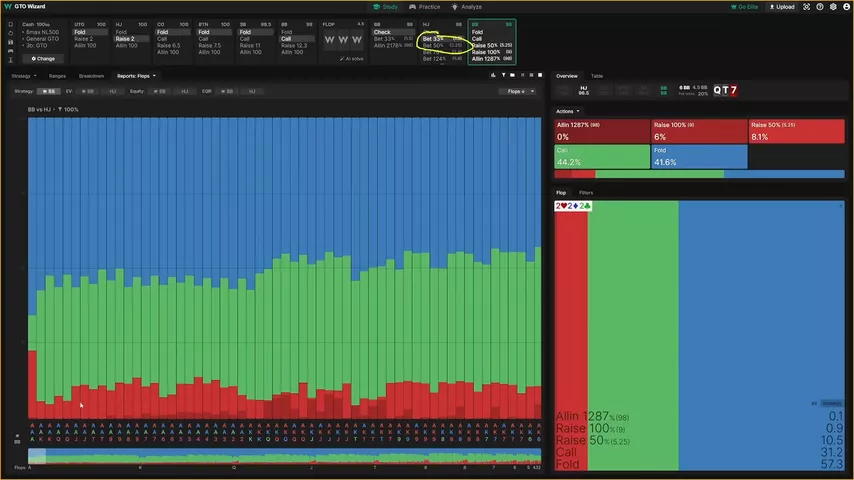
И большой блайнд фолдит в 41.6% случаев. Внимание, вопрос: какова минимальная частота защиты игрока на ББ против ставки 1.5 бб в банк 4.5 бб?
Альфа = 1.5 / (1.5 + 4.5) = 25% (фолд)
MDF = 1 – альфа = 75% (защита)
Если вы посчитали правильно, у вас должно было получиться, что «наивная» MDF большого блайнда равна 75%. Но солвер фолдит намного больше!
Что происходит? Солвер – жуткий нит?
Давайте найдём флоп, на котором ББ защищается шире всего. Таким флопом будет . Однако даже на нём ББ фолдит 27.8% рук.
Причина, на самом деле, очень логична. Возьмём какой-нибудь флоп, пусть будет , и посмотрим на эквити самой слабой руки в диапазоне хайджека против диапазона ББ. – ну да, не очень-то смотрится на таком флопе. Тем не менее её эквити составляет 21.8%. Это значит, что даже с префлоп-рэйзер может прочекать следом и реализовать часть эквити. Получается, на флопе у него нет чистых блефов.
Как вы помните, MDF предназначена, чтобы сделать соперника безразличным при выборе между блефом и чеком. Но даже со слабейшей рукой в диапазоне хайджека EV чека довольно велико – 1.66 бб. Если вы начнёте отчаянно защищаться, чтобы EV блефа с стало равно нулю, оппонент просто перестанет с ней блефовать и будет спокойно реализовывать эквити через чек, одновременно уничтожая вас доборными ставками с другими руками.
Так что когда поле оверфолдит на контбет по сравнению с MDF, оно поступает правильно.
Теперь обратимся ко второму пункту. Посмотрим сводную статистику по всем флопам для случая, когда хайджек поставил контбет 1.5 бб и получил рэйз 9 бб. Сначала посчитайте MDF: насколько широко должен защищаться хайджек?
Альфа = 9 / (9 + 6) = 60% (фолд)
MDF = 1 – альфа = 40% (защита)
Если математика вас не подвела, вы взяли количество фишек, которыми рискует ББ, и разделили на риск + награду. Получается, большому блайнду нужно, чтобы хайджек фолдил в 60% случаев. На защиту остаётся 40%.
На практике ничего подобного не происходит.
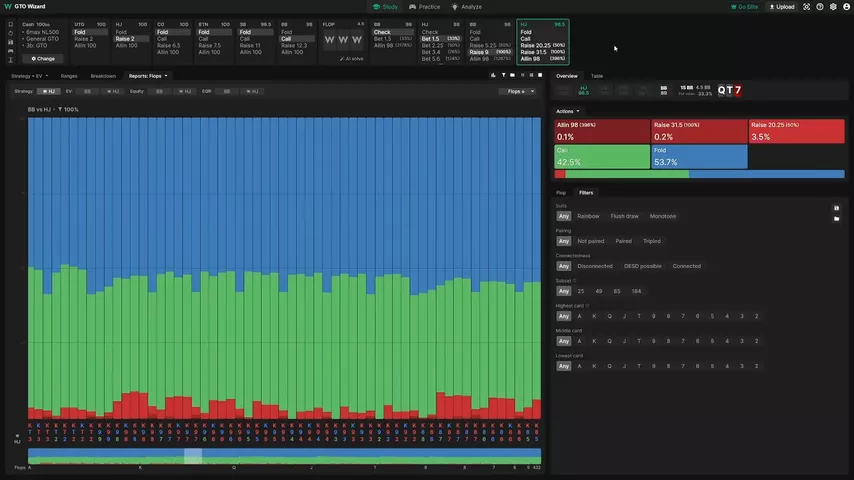
Хайджек фолдит заметно меньше 60% и коллирует шире 40%. Если люди в вашей базе защищаются от рэйза шире, чем диктует MDF, они правы.
Для иллюстрации я взял флоп .
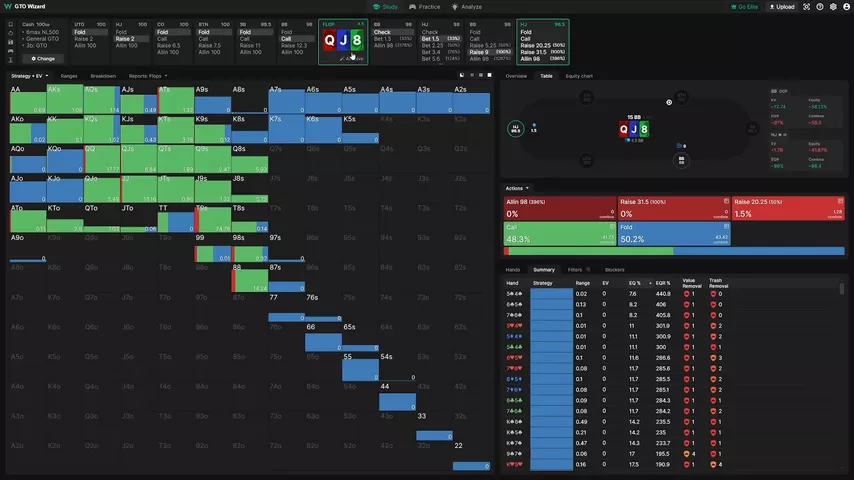
Хайджек коллирует рэйз заметно шире 40%. И причина в том, что у блефов есть эквити.
Отсортируем диапазон ББ и найдём руку с самым низким эквити. Этой рукой будут – но даже у них есть 8.4% эквити! Не слишком часто, но она тоже может выиграть банк на вскрытии.
Если хайджек начнёт фолдить по MDF, игрок на ББ, который сейчас всегда фолдит , сможет с ней чек-рэйзить! Ведь оппонент сфолдит достаточно часто, чтобы EV блефа получилось нулевым, а дальше мы получим фриролл на дополнительные 8.4% эквити, начиная с тёрна. И то же касается всех рук, которые ББ фолдит на контбет. Сейчас он фолдит все комбинации A4s – а ведь у них целых 25% эквити. Почему бы не сделать с ними рэйз в блеф?
Вся эта история с блефами, которые имеют эквити, будет происходить на всех улицах до ривера. Частота защиты по GTO против рэйза всегда будет больше MDF, потому что мы не должны давать блефам фриролл на величину их эквити.
Теперь я воспользуюсь комплексным отчётом, который показывает реакцию на максимально широкий набор сайзингов и отлично подходит для моей задачи. Его нужно активировать в опциях GTO Wizard (пиктограмма в правом верхнем углу).
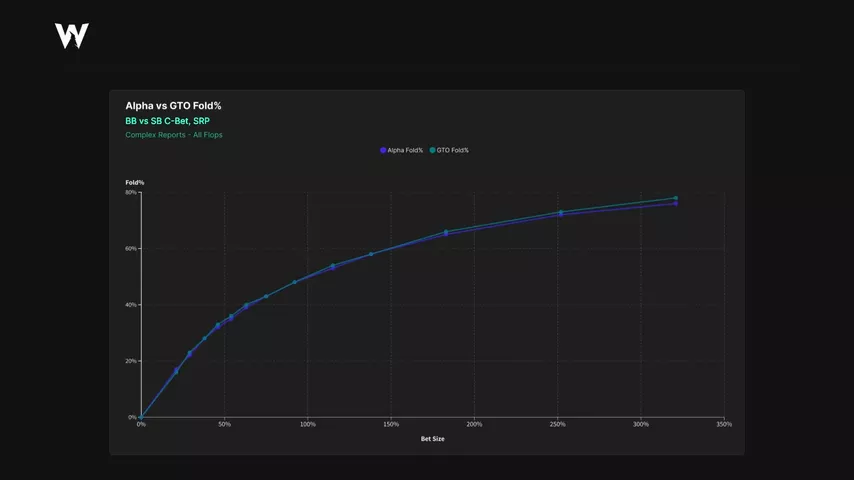
Получив нужные мне данные, я строю график, на котором сравниваю процент фолда по GTO с процентом фолда по MDF в зависимости от сайзинга контбета.
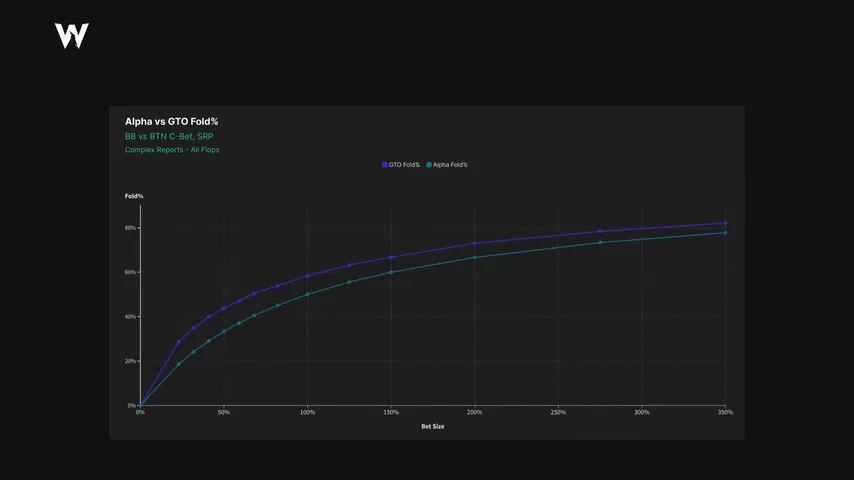
Как и ожидалось, большой блайнд всегда фолдит больше MDF (синяя линия против голубой линии) вне зависимости от сайзинга.
Проблема решена?
Давайте сменим позиции и посмотрим, как большой блайнд реагирует на контбеты малого блайнда.
Поняли, в чём разница? В этом примере большой блайнд находится в позиции. А позиция даёт преимущество. Находясь в позиции, ББ защищается почти в строгом соответствии с MDF.
Так что если ваша цель – игра по GTO, вам следует оверфолдить без позиции и играть близко к MDF, будучи в позиции.
Математика истинной MDF

Расчёт EV чистого блефа (блефа с нулевым эквити) довольно прост:
EV = (частота фолда * размер банка) – (частота колла * размер нашего блефа)
Когда мы ставим два банка на ривере, мы вынуждаем соперника защищать 34% его рук. Как только он начинает оверфолдить, наш блеф печатает деньги. Защищается шире – блеф теряет деньги.
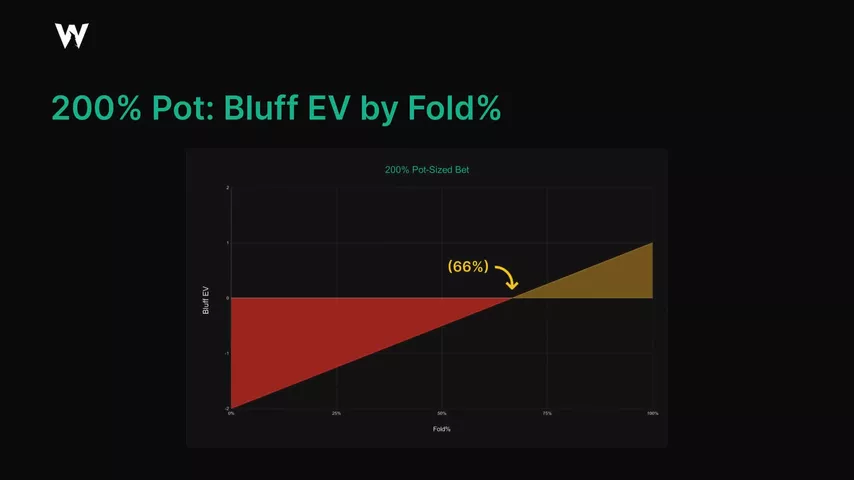
Когда мы ставим 2/3 банка, соперник должен защищаться несколько шире – не 34%, а 60%. Формула элементарная.
Однако всё меняется, когда мы принимаем, что у блефов есть эквити.
Сравним наивную MDF и истинную MDF:

Блефы, получившие колл, всегда проигрывают.
Чек всегда проигрывает.
Единственный способ выиграть – заставить оппонента сфолдить.
EV блефа = 0
– Блефы, получившие колл, сохраняют некоторое эквити
– EV чека выше нуля
– Блеф можно отложить до следующей улицы
– EV блефа = EV чека
Предположим, вы оказались на ривере с рукой, которая иногда выиграет на вскрытии. Например, со слабой карманкой, бьющей некоторые руки соперника. Вы размышляете, не превратить ли её в блеф, поставив полбанка.
Допустим, ваша рука выиграет на вскрытии в 25% случаев. Насколько часто должен фолдить оппонент, чтобы ваш блеф стал выгоднее чека?
EV блефа = EV чека = 25%
25% = частота фолда * банк – частота колла * размер ставки
25% = (1 – х) (1) – 0.5х
Искомая частота колла – 50%.
Наивная MDF считает ожидание чека равным нулю, и в этом случае оппоненту достаточно фолдить в 33.3% случаев. Однако когда у нашего блефа есть некоторая ценность, для выгодного блефа нам нужно гораздо больше фолдэквити.
На самом деле нужно учитывать не только вероятность фолда и колла, но и рэйза – против рэйза у нас тоже есть EV. Но для простоты сделаем вид, что так не бывает.
Наивная MDF: EV чека = 0:
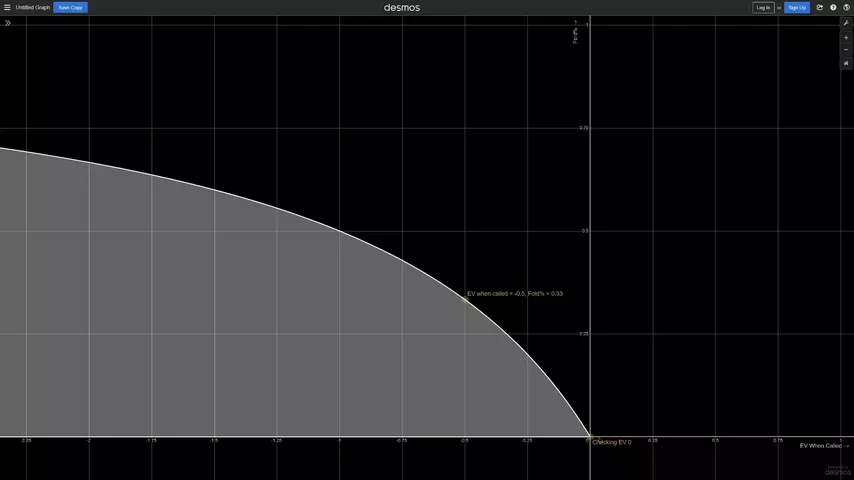
А теперь приподнимем EV чека (ось Y):
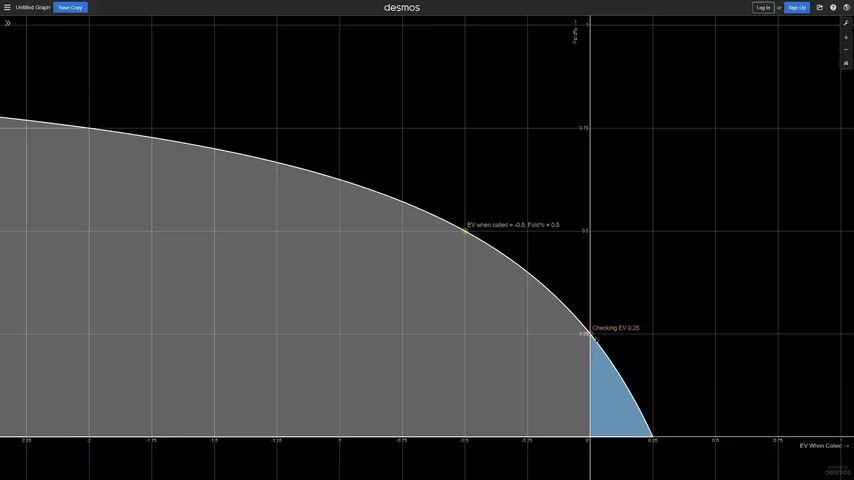
Логично: чем выше EV чека, тем больше фолдэквити нам нужно для плюсового блефа.
Обратите внимание на синюю зону справа от оси Y: это руки, ставка с которыми является доборной, то есть имеет положительное матожидание, однако чек с ними выгоднее. Не любое +EV-действие оптимально.
Золотое сечение?!?!
Напоследок небольшой бонус.
Солверную частоту защиты против рэйза на флопе, как ни странно, можно найти по довольно простой формуле, в одно действие:
% фолда по GTO против рэйза примерно равен шансам банка * золотое сечение: 1.618
Не представляю себе, откуда взялась эта зависимость, но она работает – разница с фактической величиной составляет всего 2-3%.
Допустим, мы поставили треть банка и получили рэйз размером в половину банка. Шансы банка – 25%. Примерная частота фолда = 0.25*1.618 = 0.4045 или 40.6%. Истинная частота фолда по GTO = 38.3%.
Возьмём рэйз размером в полный банк. Шансы банка – 33%. Расчётная частота = 0.33*1.618 = 0.538794 или 53.9%. Истинная частота = 54.3%.
Чудеса!
